ضریب
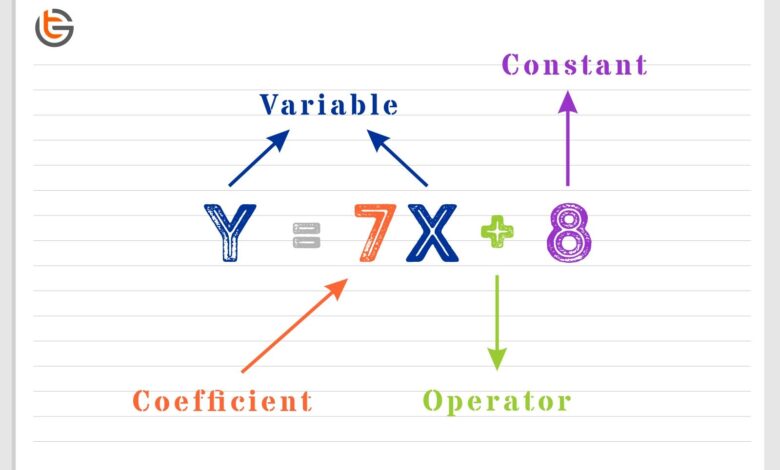
عنوان: در جستجوی مفهوم “ضریب”: کلیدی برای درک روابط ریاضی
ضریب، واژهای که با خود دنیایی از معانی و کاربردها را به همراه دارد، در واقع تنها یک عدد نیست، بلکه نمادی از ارتباطات پیچیده ریاضی، علمی و حتی اجتماعی است. از معادلات ساده گرفته تا مفاهیم پیشرفتهتر در آمار و اقتصاد، ضریب به ما کمک میکند تا نحوهی ارتباط متغیرها را درک کنیم و تحلیلهای دقیقی از دادهها ارائه دهیم. در این مقاله، به بررسی ابعاد مختلف ضریب خواهیم پرداخت؛ از تعریف و انواع آن گرفته تا نقش بسیار حیاتیاش در تسهیل فهم پدیدههای دنیای اطراف ما. با ما همراه باشید تا در این سفر سرگرمکننده و آموزنده، به عمق این مفهوم جذاب نفوذ کنیم.
ضریب و اهمیت آن در تحلیلهای مالی و اقتصادی
در دنیای مالی و اقتصادی، ضریب به عنوان یک مفهوم کلیدی شناخته میشود که توانایی تبیین روابط پیچیده بین متغیرهای مختلف را دارد. این ضریب نه تنها به تحلیلگران کمک میکند تا رفتار بازارها را پیشبینی کنند، بلکه میتواند در تصمیمگیریهای کلان اقتصادی نیز مؤثر واقع شود. به عبارت دیگر، فهم و شناخت ضریب به سرمایهگذاران امکان میدهد که نوسانات قیمتها و بازدههای مورد انتظار را تحلیل کرده و ریسکهای موجود را بهتر مدیریت کنند. موارد زیر اشارهای به اهمیت این مفهوم دارند:
- تحلیل روابط بین متغیرها: ضریبها میتوانند نشان دهند که چگونه عوامل مختلف مانند نرخ بهره یا تورم بر یکدیگر تأثیر میگذارند.
- پیشبینی عملکرد بازار: با فهم ضریبها، میتوان الگوهای حرکتی در بازار را شناسایی و پیشبینی کرد.
- مدیریت ریسک: شناخت دقیق از ضریبها به سرمایهگذاران کمک میکند تا ریسکهای بالقوه را شناسایی و ارزیابی کنند.
این ضریبها میتوانند در قالب جداول و نمودارهای مختلف معرفی شوند. به طور مثال، یک جدول ساده میتواند رابطه بین تغییرات اقتصادی و اثر آن بر روی سرمایهگذاریها را نشان دهد. در زیر یک نمونه جدول با محتوایی ساده و مفید ارائه میشود:
| متغیر | ضریب تأثیر |
|---|---|
| نرخ بهره | 0.75 |
| تورم | 0.60 |
| اعتماد مصرفکننده | 0.50 |
با درک بهتر از ضریبها و نحوه تأثیرگذاری آنها بر تصمیمات اقتصادی، میتوان به ایجاد استراتژیهای مؤثرتری برای سرمایهگذاری و اداره مالی دست یافت. برای اطلاعات بیشتر در این زمینه به این لینک مراجعه کنید.

تأثیرات متقابل ضریب در ارزیابی ریسک و بازدهی
فرمولهای مالی مانند ضریب بهعنوان ابزاری برای اندازهگیری روابط بین ریسک و بازدهی در بازارهای مالی عمل میکنند. در این راستا، میتوان با افزایش یا کاهش ضریب، تاثیرات عمیقی بر ارزیابی سرمایهگذاریها داشت. بهعنوان مثال، افزایش ضریب به معنای افزایش نوسانات و بنابراین، افزایش ریسک است. این میتواند به سرمایهگذاران این امکان را بدهد که بازدهی بالاتری را هدفگیری کنند اما در عوض، ریسک بالاتری نیز به همراه دارد. این دگرگونیها در نهایت منجر به تغییر در تصمیمگیریهای مالی و استراتژیهای سرمایهگذاری میشود.
علاوه بر این، ارزیابی ضریب در تحلیلهای فنی و بنیادی میتواند به سرمایهگذاران کمک کند تا موقعیتهای بازار را بهتر درک کنند. از طریق ایجاد روابط بین متغیرها، میتوان به سادگی فرآیند تصمیمگیری را سادهتر و قابل پیشبینیتر کرد. در این راستا، برخی از عوامل کلیدی که باید در نظر گرفته شوند عبارتند از:
- نرخ بهره
- بزرگی سرمایهگذاری
- میزان نوسانات بازار
- موقعیت جغرافیایی و اقتصادی
به طور کلی، درک این که چگونه ضریب میتواند بر ارزیابی ریسک و بازده تأثیر بگذارد، به سرمایهگذاران کمک میکند تا تصمیمات آگاهانهتری اتخاذ کنند، به گونهای که همواره بهترین نتیجه را از سرمایهگذاریهای خود بدست آورند. برای مشاوره و اطلاعات بیشتر در این زمینه میتوانید به وبسایت بت ریوراد مراجعه کنید.

راهکارهای بهبود ضریب در مدیریت سرمایهگذاری
به منظور افزایش ضریب در مدیریت سرمایهگذاری، توجه به تحلیل جامع بازار از اهمیت ویژهای برخوردار است. با استفاده از روشهای تحلیلی مانند SWOT، میتوان نقاط قوت، ضعف، فرصتها و تهدیدهای موجود در بازار را شناسایی کرد. به این ترتیب، سرمایهگذاران میتوانند از تصمیمگیری مبتنی بر داده بهرهمند شوند و استراتژیهای بهتری برای ورود به بازار انتخاب کنند. همچنین، بررسی روندهای تاریخی و پیشبینی متغیرهای اقتصادی میتواند به عنوان یک ابزار حیاتی در کمک به سرمایهگذاران در شناخت بهتر آینده عمل کند.
ایجاد یک پرتفوی متنوع نیز میتواند یکی از راهکارهای موثر در بهبود ضریب باشد. این تنوع شامل سرمایهگذاری در انواع داراییها مانند سهام، املاک، و محصولات مالی مختلف میشود. همچنین، توجه به مدیریت ریسک و تنظیم نسبتهای ریسک به بازده در هر سرمایهگذاری، به برقراری تعادل میان ریسک و پاداش کمک میکند. به طور کلی، اجرای برنامههای آموزشی و مشاورهای برای سرمایهگذاران میتواند منجر به ارتقاء دانش مالی آنها و در نتیجه بهبود عملکرد سرمایهگذاریها گردد. برای کسب اطلاعات بیشتر میتوانید به این لینک مراجعه کنید.
نقش ضریب در تصمیمگیریهای کارآفرینی و خلق ارزش
در دنیای کارآفرینی، ضریب به عنوان یک عامل کلیدی در تصمیمگیریها و پیادهسازی استراتژیها شناخته میشود. این ضریب میتواند به شکلهای مختلفی نمود پیدا کند، از جمله در تحلیل ریسک، ارزیابی بازار و سنجش نوآوری. به این ترتیب، ایجاد یک قابلیت مدیریت ضریب میتواند کارآفرینان را قادر سازد تا در شرایط ناهموار بازار تصمیمات بهتری اتخاذ کنند. در این راستا، کارآفرینان باید به دنبال ابزارها و تکنیکهای تحلیلی باشند که به آنها در تعیین و بررسی ضریب کمک کند، از جمله دادههای تحقیقاتی، پیشبینیهای مالی و بررسی رفتار مصرفکننده.
به علاوه، ضریب میتواند به کارآفرینان این امکان را بدهد که در فرآیند خلق ارزش، رویکردهای خلاقانهتری را به کار ببرند. به عنوان مثال، استفاده از مدلهای تحلیلی برای تعیین اینکه کدام محصولات محبوبتر خواهند بود یا کدام نوع خدمات به نیاز مشتریان بهتر پاسخ میدهد، میتواند به بالابردن ضریب موفقیت منجر شود. بنابراین، کارآفرینان میبایست به تحقیق و توسعه در زمینه این ضریب توجه کنند و به دنبال ابداعات و تغییرات مستمر در محصولات و خدمات خود باشند. برای اطلاعات بیشتر میتوانید به وبسایت Betreward مراجعه کنید.
سوال و جواب
پرسش و پاسخ درباره “ضریب”
پرسش ۱: ضریب چیست و در چه زمینههایی کاربرد دارد؟
پاسخ: ضریب یک مفهوم ریاضی و علمی است که به نسبت یا اندازهگیری در یک زمینه خاص اشاره دارد. این واژه بهطور گستردهای در علوم مختلف از جمله ریاضیات، اقتصاد، فیزیک و حتی علوم اجتماعی استفاده میشود. به عنوان مثال، در ریاضیات، ضریب ممکن است به عددی اشاره کند که در کنار یک متغیر قرار دارد، مانند ۲x که در آن ۲ ضریب x است. در اقتصاد، ضریب نمونهای از نسبتهای مختلف مانند “ضریب جینی” است که نشاندهنده توزیع درآمد در جامعه میباشد.
پرسش ۲: آیا ضریب همیشه عددی مثبت است؟
پاسخ: خیر، ضریب ممکن است مثبت یا منفی باشد و به مفهوم خاص زمینه بستگی دارد. برای مثال، در معادلات فیزیکی، ضریب میتواند منفی باشد و به این معنی باشد که یک اثر مخالف در حال وقوع است. بنابراین، بسته به نوع معادله و شرایط، ضریب میتواند انواع مختلفی از مقادیر را به خود بگیرد.
پرسش ۳: چگونه میتوان ضریب را محاسبه کرد؟
پاسخ: روند محاسبه ضریب بسته به نوع آن متفاوت است. برای مثال، در یک معادله خطی دو متغیره، ضریب متغیرها از طریق روشهای آماری مانند رگرسیون خطی محاسبه میشود. در علوم اجتماعی، ممکن است از دادههای نظرسنجی برای محاسبه ضریبهای اقتصادی یا اجتماعی بهره بگیریم. به طور کلی، برای محاسبه ضریب، لازم است دادههای لازم جمعآوری و تجزیه و تحلیل شوند.
پرسش ۴: آیا میتوان بهطور خاص به ضریبهای اقتصادی اشاره کرد؟
پاسخ: بله، در حوزه اقتصاد، ضریبها نقشی اساسی دارند. بهعنوان مثال، “ضریب جینی” برای سنجش نابرابری درآمدی مورد استفاده قرار میگیرد و “ضریب اشتغال” نشاندهنده نسبت نیروی کار شاغل به کل نیروی کاری است. این ضریبها به تحلیلهای اقتصادی کمک کرده و به تصمیمگیرندگان اطلاعات ارزشمندی درباره وضعیت اقتصادی ارائه میدهند.
پرسش ۵: آیا میتوان از ضریبهای علمی در زندگی روزمره استفاده کرد؟
پاسخ: بله، ضریبها در زندگی روزمره نیز کاربردهایی دارند. برای مثال، در مقادیر مختلف تغذیه، ضریبهای مختلفی برای مواد غذایی وجود دارد که میتواند به ما در انتخاب غذای سالمتر کمک کند. همچنین در محاسبات مالی، ضریبهای بهره وامها و سپردهها بر تصمیمگیریهای مالی افراد تأثیر میگذارد. بهطور کلی، درک ضریبها میتواند به بهینهسازی انتخابها و تصمیمگیریهای روزمره کمک کند.
پرسش ۶: آیا ضریبهای اجتماعی نیز وجود دارند؟
پاسخ: بله، ضریبهای اجتماعی وجود دارند که به تحلیل و درک دینامیکهای اجتماعی کمک میکنند. مانند “ضریب همبستگی” که نشاندهنده ارتباط بین دو یا چند متغیر اجتماعی است. اینگونه ضریبها به محققان و سیاستگذاران کمک میکند تا پیامدهای اجتماعی و فرهنگی مختلف را ارزیابی کنند و به تصمیمگیریهای بهتری در زمینه سیاستگذاری اجتماعی برسند.
—
امیدواریم این پرسش و پاسخها به روشنشدن مفهوم “ضریب” کمک کند و اطلاعات مفیدی را در اختیار شما قرار دهد.
Wrapping Up
در این مقاله به بررسی مفهوم “ضریب” پرداختهایم و جوانب مختلف آن را در زمینههای گوناگون علمی و عملی مورد تحلیل و بررسی قرار دادهایم. از ریاضیات گرفته تا اقتصاد و علوم اجتماعی، ضریبها نقش بسزایی در تبیین و تحلیل پدیدههای مختلف ایفا میکنند. با درک عمیقتر از این مفهوم، نه تنها میتوانیم تحلیلهای دقیقتری ارائه دهیم، بلکه به سادگی میتوانیم در تصمیمگیریهای روزمره خود از آن بهرهمند شویم. امیدواریم این مقاله توانسته باشد درک شما را از ضریب و کاربردهای آن گسترش دهد و به ارائه نگاهی نوین به این موضوع کمک کند. بیتردید، جهان اطراف ما سرشار از ضریبهاست که هر یک داستانی را روایت میکنند. پس بیایید با کنجکاوی بیشتر به کاوش در این دنیای ریاضی و مفهومی ادامه دهیم.






